Список голосов Thank You

[iPhonograph]

3) e

Реквестирую немного математики (решение).

Пусть N(x) = мат.ожидание количества прогулок, необходимых чтобы набрать x вёдер воды, 0<=x<=1
Пусть за первую прогулку блондинка донесла z вёдер воды, 0<z<1
С вероятностью (1-x) блондинка принесёт достаточное количество воды z>x, и ей хватит всего одной прогулки
Если z<x, то кроме этой одной прогулки потребуются ещё N(x-z) прогулок, чтобы принести ещё (x-z) вёдер воды

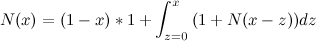
Упростим:

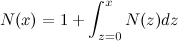
Отсюда видно, что N(0)=1, а продифференцировав, получим N'(x) = N(x)
Решение этого дифура всем известно: N(x) = exp(x)
Поэтому N(1) = e