XV тур Математического марафонаВладимир Лецко начинает новый тур
//текст доступен после регистрации//. От меня в этот раз в нём всего одна задача, так что буду осуществлять в основном информационную поддержку.
Задачи очень интересные, за короткой формулировкой открывается широкий простор для мысли. Есть, чем заняться на каникулах

Решения можно присылать на
val@dxdy.ru (в этом случае его сразу увидят оба ведущих), на
val-etc@yandex.ru или в ЛС.
Не забывайте высылать вместе с решениями свои эстетические оценки задач.
==================================Решения принимаются до
10.09.11ММ141 (3 балла)
Существуют ли натуральные числа n такие, что
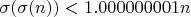
?
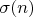
- сумма натуральных делителей числа n.
==================================Решения принимаются до
14.09.11ММ142 (4 балла)
Все 80 натуральных делителей натурального числа n расположили в порядке возрастания. Оказалось, делители с первого по четвертый образуют геометрическую прогрессию, делители с четвертого по седьмой - арифметическую прогрессию, а восьмой делитель меньше 200.
Найти n.
==================================В
Тематическом конкурсе тура - вновь
комбинаторная геометрия.
Более того, во всех тематических задачах, кроме КГ-11, речь вновь пойдет о многоугольниках. Но на этот раз - не обязательно выпуклых.
==================================Решения принимаются до
18.09.11ММ143 (КГ-11) (4 балла)
Девять из десяти ребер пятиугольной пирамиды имеют длину 1. В каком диапазоне может изменяться длина 10-го ребра?
==================================Решения принимаются до
23.09.11ММ144 (5 баллаов)
На поле e4 стоит чёрный король. Первый игрок ставит на любую клетку доски, не находящуюся под боем чёрного короля, белых королей (по одному за ход). Второй игрок делает (правильный) ход чёрным королём. Игра заканчивается, когда у чёрного короля не будет ходов. Каково минимальное количество ходов, за которое первый игрок может достичь цели?
==================================В задачах КГ-12 - КГ-15 будем придерживаться следующих определений и обозначений:
Под многоугольником мы будем понимать плоскую замкнутую несамопересекающуюся ломаную, никакие три последовательные вершины которой не коллинеарны. Число сторон исходного многоугольника обозначим через n.
Назовем сторону многоугольника свободной, если продолжение этой стороны за каждую ограничивающую ее вершину в некоторой окрестности этой вершины лежит вне многоугольника.
Назовем сторону полусвободной, если вне многоугольника лежит продолжение стороны ровно за одну из двух ограничивающих ее вершин. Сторону, не являющуюся ни свободной, ни полусвободной, будем называть зажатой. Например, сторона AB (рис. 1), является свободной, сторона BC - полусвободной, а сторона EF - зажатой.
Диагональ, все точки которой принадлежат многоугольнику, будем называть внутренней. Диагональ, не имеющую с многоугольником общих точек, за исключением вершин, которые она соединяет, будем называть внешней. Например, диагональ BF (рис. 1) - внутренняя, а диагональ BD - внешняя (диагональ BE не является ни внешней, ни внутренней).
//текст доступен после регистрации// ==================================Решения принимаются до
27.09.11ММ145 (КГ12) (3 балла)
Сколько внешних диагоналей может иметь n-угольгик?
==================================Решения принимаются до
1.10.11ММ146 (4 балла)
При каких D существуют графы диаметра D, у которых сумма квадратов степеней вершин равна D
2?
==================================Решения принимаются до
7.10.11ММ147 (КГ13) (6 баллов)
Какое наименьшее число внутренних диагоналей может иметь n-угольгик, у которого ровно один угол больше развернутого?
==================================Решения принимаются до
15.10.11ММ148 (КГ14) (8 баллов)
Сколько внутренних диагоналей может иметь n-угольгик?
==================================Решения принимаются до
22.10.11ММ149 (8 баллов).
При каком наименьшем n в группе перестановок S
n существует подгруппа порядка 253? Привести пример такой подгруппы.
Примечание: Задачу можно решить на бумажке, без компьютерного перебора
==================================Решения принимаются до
31.10.11ММ150 (КГ15) (12 баллов)
Каждому n-угольнику поставим в соответствие ожерелье из n бусин белого, зеленого и красного цветов следующим образом: свободой стороне соответствует белая бусина; полусвободной - зеленая; зажатой - красная.
Два n-угольника назовем эквивалентными, если им соответствуют одинаковые ожерелья (ожерелье не меняется при поворотах и переворачивании). На сколько классов эквивалентности разобьются 20-угольники?
