|
Руслан Дехтярь
Гость
|
 |
� Ответ #45 : Январь 12, 2015, 11:00:06 � |
|
6 6 6 6 6 +6 6 6 = 67 332
|
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #46 : Январь 12, 2015, 11:27:44 � |
|
6 6 6 6 6 +6 6 6 = 67 332
подскажите как решать такие задачи? кроме как методом перебора - не получается? |
|
|
|
|
 Записан
Записан
|
|
|
|
dektig
Свой человек
  
 Offline Offline
Сообщений: 357
СПАСИБО
-вы поблагодарили: 154
-вас поблагодарили: 178

|
 |
� Ответ #47 : Январь 12, 2015, 12:59:33 � |
|
7 7 7- 7 7* 7/ 7 = 700
7 *(7/ 7+ 7 /7 +7* (7+ 7) = 700
2*( 2 2 2/ 2- 2 2/ 2) = 200
4 4 4- 4+ 4 4 -4+ 4* 4+ 4 = 500
6* 6/ 6( 6 6 6/ 6- 6 6/6) = 600
9 9 9- 9+ (9* 9+9)/ 9* 9/ 9 = 1000
|
|
|
|
|
 Записан
Записан
|
|
|
|
dektig
Свой человек
  
 Offline Offline
Сообщений: 357
СПАСИБО
-вы поблагодарили: 154
-вас поблагодарили: 178

|
 |
� Ответ #48 : Январь 12, 2015, 13:05:06 � |
|
Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола.
Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Сначала нужно заполнить места по гендерному принципу, потом бесполые. Для Ж=6*5*4*3=260 Для М= 8*7*6*5*4*3=20160 Для Б=4*3*2=24 Всего 260+20160+24=20444 способов Наверно так) |
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #49 : Январь 12, 2015, 16:49:53 � |
|
Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола.
Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Сначала нужно заполнить места по гендерному принципу, потом бесполые. Для Ж=6*5*4*3=260 Для М= 8*7*6*5*4*3=20160 Для Б=4*3*2=24 Всего 260+20160+24=20444 способов Наверно так) неа, верный ответ 1680 вариантов. Но как к нему прийти??? |
|
|
|
|
 Записан
Записан
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #50 : Январь 12, 2015, 17:07:07 � |
|
нашла в интернете, что вот такая формула подходит, но яне понимаю как ее приминить //текст доступен после регистрации// |
|
|
|
|
 Записан
Записан
|
|
|
|
dektig
Свой человек
  
 Offline Offline
Сообщений: 357
СПАСИБО
-вы поблагодарили: 154
-вас поблагодарили: 178

|
 |
� Ответ #51 : Январь 12, 2015, 21:39:27 � |
|
нашла в интернете, что вот такая формула подходит, но яне понимаю как ее приминить //текст доступен после регистрации//нет. по ней еще больше результат получится. Вероятно, нужно применить формулу сочетания 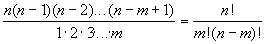 ))а по ней получится 15+28+364=407 |
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #52 : Январь 12, 2015, 21:55:01 � |
|
Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на
первую специальность, то есть 4 женщин из 6:
C4/6 = 6!/4! · 2! = 15.
Далее независимо аналогичным образом выберем мужчин на вторую специальность:
C6/8 = 8!/6! · 2! = 28
хоть убейте не понимаю как 15 и 28 получайется...
|
|
|
|
� Последнее редактирование: Январь 12, 2015, 22:22:12 от Yana_2783 �
|
 Записан
Записан
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #53 : Январь 14, 2015, 23:00:00 � |
|
новые задачи на пятницу утро  : 1) На доске написаны все натуральные числа от 1 до 2015 – некоторые числа красным маркером, а остальные – синим. Наибольшее синее число равно количеству синих чисел, наименьшее красное число – в два раза меньше количества красных чисел. Сколько красных чисел написано на доске? 2) Карлсон поставил на шахматную доску несколько фишек (в каждую клетку – не более одной), причём на каждой горизонтали и вертикали оказалось не менее двух фишек. Всегда ли Малыш может убрать несколько из них так, чтобы на каждой горизонтали и вертикали осталось ровно по одной фишке? 3) верна ли такая теорема: Пусть даны два многоугольника, имеющие равные площади. Тогда один из них можно разрезать на 10 частей и сложить из них другой многоугольник. |
|
|
|
� Последнее редактирование: Январь 14, 2015, 23:03:23 от Yana_2783 �
|
 Записан
Записан
|
|
|
|
Smith
Из мудрейших мудрейший
 
 Offline Offline
Сообщений: 2950
СПАСИБО
-вы поблагодарили: 286
-вас поблагодарили: 307
PeAcE

|
 |
� Ответ #54 : Январь 15, 2015, 12:04:00 � |
|
новые задачи на пятницу утро  : 1) На доске написаны все натуральные числа от 1 до 2015 – некоторые числа красным маркером, а остальные – синим. Наибольшее синее число равно количеству синих чисел, наименьшее красное число – в два раза меньше количества красных чисел. Сколько красных чисел написано на доске? С + (С+1)*2 = 2015 К = 2015 - С К = 1344 |
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #55 : Январь 16, 2015, 08:51:28 � |
|
2) Карлсон поставил на шахматную доску несколько фишек (в каждую клетку – не более одной), причём на каждой горизонтали и вертикали оказалось не менее двух фишек. Всегда ли Малыш может убрать несколько из них так, чтобы на каждой горизонтали и вертикали осталось ровно по одной фишке?
3) верна ли такая теорема: Пусть даны два многоугольника, имеющие равные площади. Тогда один из них можно разрезать на 10 частей и сложить из них другой многоугольник.
|
|
|
|
|
 Записан
Записан
|
|
|
|
dektig
Свой человек
  
 Offline Offline
Сообщений: 357
СПАСИБО
-вы поблагодарили: 154
-вас поблагодарили: 178

|
 |
� Ответ #56 : Январь 16, 2015, 12:00:24 � |
|
2.Не всегда. Например, в такой ситуации:
* *
* *
* *
* * * * * * * *
* * * * * * * *
* *
* *
* *
|
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #57 : Январь 16, 2015, 12:10:36 � |
|
а как доказать теорему? сын написал:"Возьмем теаорему Пифагора. Если две фигуры можно разрезать на одинаковые наборы частей, то эти фигуры называются равносоставленными. Равносоставленные фигуры, разумеется, равновелики – они имеют равные площади. Для многоугольников верна и обратная теорема: любые два равновеликих многоугольников равносоставлены. Разрезанием и складыванием невозможно изменить площадь. " мне кажется ,что это не доказательство. не хватает аргументов. может надо нарисовать прямоугольник и разрезать его на 3 части к примеру. А потом сделать вывод, что если разрезать прямоугольник на любое коеличесиво фигур и сложить из эти фигур любую фигуру - площадь не изменится.  |
|
|
|
|
 Записан
Записан
|
|
|
|
Yana_2783
Новенький

 Offline Offline
Сообщений: 48
СПАСИБО
-вы поблагодарили: 28
-вас поблагодарили: 1

|
 |
� Ответ #58 : Январь 16, 2015, 12:12:46 � |
|
2.Не всегда. Например, в такой ситуации:
* *
* *
* *
* * * * * * * *
* * * * * * * *
* *
* *
* *
а если Х-образно их на доске располагать - ведь тоже невозможно? |
|
|
|
|
 Записан
Записан
|
|
|
|
dektig
Свой человек
  
 Offline Offline
Сообщений: 357
СПАСИБО
-вы поблагодарили: 154
-вас поблагодарили: 178

|
 |
� Ответ #59 : Январь 16, 2015, 20:32:34 � |
|
2.Не всегда. Например, в такой ситуации:
* *
* *
* *
* * * * * * * *
* * * * * * * *
* *
* *
* *
а если Х-образно их на доске располагать - ведь тоже невозможно? возможно. 3. Возьмем равновеликие квадрат и 20тиконечную звезду. 10 частей ни там, ни там вырезать не получится)) |
|
|
|
|
 Записан
Записан
|
|
|
|
|
