Кубики, занумерованные числами 1,2,... кладутся в безразмерный ящик следующим образом.
За одну минуту до полудня кладутся кубики от 1 до 10, и кубик 1 вынимается обратно.
За 1/2 минуты до полудня кладутся кубики от 11 до 20, и кубик 2 вынимаетсяобратно.
За 1/3 минуты до полудня кладутся кубики от 21 до 30, и кубик 3 вынимается обратно.
И т.д.
Сколько кубиков останется в ящике в полдень?
|
Um_nik
Гость
|
 |
� Ответ #15 : Ноябрь 22, 2010, 12:17:14 � |
|
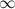 - не число |
|
|
|
|
 Записан
Записан
|
|
|
|
ra_miros
Новенький

 Offline Offline
Сообщений: 15
СПАСИБО
-вы поблагодарили: 0
-вас поблагодарили: 0


|
 |
� Ответ #16 : Ноябрь 22, 2010, 12:33:04 � |
|
Мы можем кубики заменить числами и найти предел?
Тогда получается что после n-й итерации остается 9n кубиков
Можно построить формулу, определяющую кол-во кубиков в любой момент времени между 11:59:00 и 12:00:00 (не включая)
f(t) = [1/(1-t)]*9, 0<= t < 1
t - время в долях минуты
Например, что там накидают в 11:59:59
t = 59/60, f(t) = 540 (c 61 - го по 600-й)
В 11:59:59.990 имеем 54 000
В 11:59:59.991 имеем 59 994
и т.д.
|
|
|
|
|
 Записан
Записан
|
|
|
|
T-Mon
Гений
    
 Offline Offline
Сообщений: 889
СПАСИБО
-вы поблагодарили: 93
-вас поблагодарили: 134
Hakuna Matata!

|
 |
� Ответ #17 : Ноябрь 22, 2010, 12:37:01 � |
|
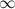 - не число Это очередной абсурд среди прочего абсурда в этой задаче. Так что ничего странного. |
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #18 : Ноябрь 22, 2010, 12:38:21 � |
|
Эта задача абсурдна с точки зрения физики. Но не с точки зрения математики.
|
|
|
|
|
 Записан
Записан
|
|
|
|
T-Mon
Гений
    
 Offline Offline
Сообщений: 889
СПАСИБО
-вы поблагодарили: 93
-вас поблагодарили: 134
Hakuna Matata!

|
 |
� Ответ #19 : Ноябрь 22, 2010, 12:49:58 � |
|
Эта задача абсурдна с точки зрения физики. Но не с точки зрения математики.
По моему скромному мнению, она абсурдна с точки зрения науки вообще. Хотя решение мне нравится самому, хоть я и не согласен с ним. С точки зрения математики верно решение, которое написал Рамирос. А ответ банален - бесконечное количество кубиков. |
|
|
|
� Последнее редактирование: Ноябрь 22, 2010, 13:04:20 от T-Mon �
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #20 : Ноябрь 22, 2010, 14:13:10 � |
|
ИМХО, твое решение верное. Только нужно что-то сделать с "отнятием" у бесконечности звания числа.
|
|
|
|
|
 Записан
Записан
|
|
|
|
T-Mon
Гений
    
 Offline Offline
Сообщений: 889
СПАСИБО
-вы поблагодарили: 93
-вас поблагодарили: 134
Hakuna Matata!

|
 |
� Ответ #21 : Ноябрь 22, 2010, 14:16:32 � |
|
Оно красивое, но я считаю его неверным. Посему отнимать я ничего не хочу.
Верным я считаю ответ - бесконечное количество.
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #22 : Ноябрь 22, 2010, 15:22:04 � |
|
Я думаю, что в любой определенный момент времени (включая полдень) в ящике будет определенное кол-во кубиков [1]. Процедура добавления 10 кубиков и вынимания 1 кубика будет производится бесконечное кол-во раз. Таким образом мы должны принять, что в полдень в ящике будет либо бесконечность кубиков (потому что мы бесконечное число раз добавляли 9 кубиков) [2], либо не будет ни одного кубика (потому что мы вынимали по одному кубику бесконечное число раз) [3]. Эти два противоположных друг другу варианта "порождают" еще один: полдень не наступит [4]. Время будет бесконечно приближаться к полудню, но никогда его не настигнет. Это напоминает апорию Зенона про Ахиллеса.
Собственно, утверждения [1] и [2] противоречат друг другу. Доказательство ложности апории Зенона про Ахиллеса я почти не понимаю, посему и не могу утверждать, что утверждение [4] ложно.
Ответ: Либо 0, либо полдень не наступит.
|
|
|
|
|
 Записан
Записан
|
|
|
|
T-Mon
Гений
    
 Offline Offline
Сообщений: 889
СПАСИБО
-вы поблагодарили: 93
-вас поблагодарили: 134
Hakuna Matata!

|
 |
� Ответ #23 : Ноябрь 22, 2010, 15:41:28 � |
|
2 Um_Nik В отличие от апории Зенона, где количество выполняемого действия уменьшается вместе с промежутком времени, в этой задаче с уменьшением промежутка времени количество действия не уменьшается, поэтому тот факт, что полдень не наступит, в этой задаче более правдоподобен. Мне представляется такой себе диафильм с бесконечным кино. Вы делаете полоборота, прокручивается кадр, вы делаете 1/6 оборота - кадр, 1/12 - кадр, 1/20 - кадр и т.д ( 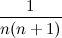 ). В пределе вы практически перестаёте крутить диафильм, а кино идёт нормальным ходом. Как итог, кино будет идти бесконечно, а оборот вы так и не сделаете никогда. Как только оборот будет сделан, нарушится условие задачи, поскольку действие пойдёт быстрее, чем положено. |
|
|
|
� Последнее редактирование: Ноябрь 22, 2010, 15:47:53 от T-Mon �
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #24 : Ноябрь 22, 2010, 15:52:44 � |
|
Ну да, я об этом тоже подумал)
|
|
|
|
|
 Записан
Записан
|
|
|
|
Димыч
Умник
   
 Offline Offline
Сообщений: 770
СПАСИБО
-вы поблагодарили: 65
-вас поблагодарили: 384

|
 |
� Ответ #25 : Ноябрь 22, 2010, 19:48:12 � |
|
При приближении к полудню число кубиков стремится к бесконечности. Но отсюда вовсе не следует, что в полдень их будет бесконечно много. В данном случае их останется 0. Здесь нет никакого противоречия.
|
|
|
|
|
 Записан
Записан
|
|
|
|
T-Mon
Гений
    
 Offline Offline
Сообщений: 889
СПАСИБО
-вы поблагодарили: 93
-вас поблагодарили: 134
Hakuna Matata!

|
 |
� Ответ #26 : Ноябрь 22, 2010, 20:20:33 � |
|
В данном случае их останется 0. Здесь нет никакого противоречия.
Какое доказательство этого ответа? |
|
|
|
|
 Записан
Записан
|
|
|
|
ra_miros
Новенький

 Offline Offline
Сообщений: 15
СПАСИБО
-вы поблагодарили: 0
-вас поблагодарили: 0


|
 |
� Ответ #27 : Ноябрь 22, 2010, 21:36:40 � |
|
При приближении к полудню число кубиков стремится к бесконечности. Но отсюда вовсе не следует, что в полдень их будет бесконечно много.В данном случае их останется 0. Здесь нет никакого противоречия.
Вы же сами себе противоречите. Теорию пределов никто не отменял. А то что мы имеем бесконечность минус бесконечность, так это не ноль, а всего лишь неопределенность, которая в данной конкретной задаче равна бесконечности |
|
|
|
|
 Записан
Записан
|
|
|
|
Илья
Высший разум
    
 Offline Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...

|
 |
� Ответ #28 : Ноябрь 22, 2010, 22:32:26 � |
|
Умные дядьки во главе с самим Джоном Литлвудом, который кстати говоря данную задачку и сформулировал, говорят, что кубиков в полдень будет ноль.
Вот наиболее краткое обоснование, которое мне понравилось, хотя пока так до конца в голове и не уложилось:
Множество кубиков, которые останутся в ящике в полдень является подмножеством множества всех кубиков (пронумрованных натуральными числами). Но при этом для любого кубика верно, что до наступления полудня он успеет оказаться в ящике и быть вынутым. Иными словами для любого кубика верно, что он не будет содержаться в ящике в полдень.
Множество "полуденных" кубиков пусто.
|
|
|
|
|
 Записан
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
Димыч
Умник
   
 Offline Offline
Сообщений: 770
СПАСИБО
-вы поблагодарили: 65
-вас поблагодарили: 384

|
 |
� Ответ #29 : Ноябрь 22, 2010, 22:47:21 � |
|
Теорию пределов никто не отменял.
Теория пределов ни при чем. В условии не сказано, что число кубиков — непрерывная функция или что-то в этом роде. Кажущееся противоречие возникает именно из-за ложной аналогии с пределами. |
|
|
|
� Последнее редактирование: Ноябрь 22, 2010, 22:50:00 от Димыч �
|
 Записан
Записан
|
|
|
|
|
