Сумашедшая старушка в самолете (вариация№2)

[Вилли ☂]

...
Старушка 1
пасажиры 2,3
места соотв 1,2,3

Варианты рассадки
Показать скрытый текст

123  +  +  +  +  +  +
132  -   -   -   -   -   -
213  +  -   +  -   -   +
231  -   -   -   -   -   +
312  +  -   -   -   -   -
321  +  +  -   -   -   +

...

если рассматривать 14 РАВНОВЕРОЯТНЫХ (?) событий, благоприятных - 6:
P(3) = 6/14= 3/7

по другому:
если рассмотреть 6 РАВНОВЕРОЯТНЫХ (!) последовательностей вариантов входа в самолёт:
P(3) = 1/6 * (1/4 + 1/2 + 1/2 + 1 + 1 + 1/4)  = 7/12

Голосую за ответ:  P(3) = 7/12

[Smith]

willi, мне кажется, что имеет место лишь три различных события:
1) Д впереди С (вероятность 1/2 - для половины всех N! возможных вариантов перестановок)
2) Д последний (вероятность1/2 - для N!/N вариантов)
3) Д не в конце, но где-то позади С (вероятность можно посчитать как-то тоже через N! (подумаю) - для ((N!/2)-(N!/N)) вариантов)

зы: вот как-то так..

[buka]

Даю совет.
Показать скрытый текст

Постарайтесь решить следующую задачу:
На самолёт проданы все N мест. Среди пассажиров имеется сумасшедшая старушка и пассажиры ведут себя как и было ранее описано.
Определить вероятность того, что предпоследний (в очереди на посадку) пассажир сядет на своё место. Старушка может быть в очереди на любом другом месте.

[Redirect]

Суровая старушка переполошила все аэропорты мира

[Вилли ☂]

willi, мне кажется, что имеет место лишь три различных события:
1) Д впереди С (вероятность 1/2 - для половины всех N! возможных вариантов перестановок)

Варианты: ДСП и ДПС
ДСП:
тогда С на своём месте с вероятност'ю 1/2 (удачно сели)

ДПС:
тогда П на своём месте с вероятност'ю 1 (удачно сели)

Итого 1) 1/2 * (1/2 + 1) = 3/4

2) Д последний (вероятность1/2 - для N!/N вариантов)

Варианты: СПД и ПСД
СПД:
тогда С на своём месте с вероятност'ю 1/3 (удачно сели)
и С не на своём месте с вероятност'ю 2/3 (не удачно сели)

ПСД:
тогда С на своём месте с вероятност'ю 1/2 (удачно сели)

Итого 2) 1/2 * (1/3 + 1/2) = 5/12

3) Д не в конце, но где-то позади С (вероятность можно посчитать как-то тоже через N! (подумаю) - для ((N!/2)-(N!/N)) вариантов)

тол'ко вариант: СДП подходит

тогда С на своём месте с вероятност'ю 1/3 (удачно сели)
и С не на своём месте с вероятност'ю 2/3 (не удачно сели)

Итого 3) 2/3

Не хватает варианта ПДС.
его вероятност' 1/6

Не знаю зачем Вы об'единили некоторые варианты, а некоторые оставили поразен'.

по моему моя табличка намного удобнее показывает все возможные варианты и все возможные вероятности.

[Smith]

вилли, я рассматриваю усложненный вариант, предложенный букой. надеюсь, ты тоже?
если да, то тогда в любом варианте ДПС или ДСП вероятность для Д сесть на свое места составляет 1, и не важно, что там дальше происходит между С и П. т.е., в 3 вариантах из 6 вероятность 1, а в целом - 1/2 для половины всех возможных случаев.
 
зы: или я чего-то не понимаю в твоем комментарии..

[Smith]

Даю совет.
Показать скрытый текст

Постарайтесь решить следующую задачу:
На самолёт проданы все N мест. Среди пассажиров имеется сумасшедшая старушка и пассажиры ведут себя как и было ранее описано.
Определить вероятность того, что предпоследний (в очереди на посадку) пассажир сядет на своё место. Старушка может быть в очереди на любом другом месте.

бука, спасибо за совет, но пока что я только еще более запутался, может завтра соберу мысли в кучу

[Smith]

Не хватает варианта ПДС.

вилли, при ПДС вероятность такая же, как при ДСП и ДПС, т.е.1) событие, т.к. С идет уже за Д и никак не может ему помешать сесть на свое место. равно как и П не мешает Д.
на счет удачно/неудачно сели - завтра вчитаюсь, сегодня просто нет ни сил, ни времени. кстати, и табличку рассмотрю внимательнее

[buka]

Я могу дать дальнейшие подсказки

[Smith]

бука, просто чуть времени не хватает, и не все складывается
например, для Джо при 3 я считал так:
1/3*1+(1/3*1/2*1+1/3*1/2*2/3)+1/3*1/2=1/2+1/6+1/9=14/18=7/9
а для 4 если считать аналогично, то у меня не получается:
1/4*1+(1/4*1/2*1+1/4*1/2*3/4)+(1/4*1/2*1+1/4*1/2*2/3)+1/4*1/2=чему-то, но не 115/144.
хотя, если считаю аналогично через количество вариантов, то получаю:
1/2+(2*3/4+4*2/3)*(1/24)+1/8=115/144
не понимаю, где ошибаюсь..
что до вопроса  - какой будет вероятность конкретно для предпоследнего пасажира, то имхо 2/3

[Smith]

но проблема даже не в расчетах. для каждого конкретного N возможно так или иначе просчитать. но пока не получается свести все расчеты в единую формулу. т.е., для Джо первый - 1/N, для Джо последний - 1/2, а для Джо от (2) до (N-1) не понятно пока как устаканить..

зы: пока что пытаюсь играться стаканами..

[Димыч]

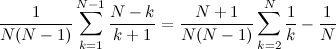Вроде так, если не ошибся.
Это вероятность, что Джо НЕ займет свое место.

[Smith]

Димыч, вопрос в том - какая вероятность, что займет.. 

зы: а что есть k? или вы о размещениях ведете речь?

[buka]

Димыч, вопрос в том - какая вероятность, что займет.. 

зы: а что есть k? или вы о размещениях ведете речь?

Не, вероятность что займёт равна 1 - вероятность, что не займёт
Я формулы скрупулёзно не проверял, но судя по подходу в параллельной теме, ответ правильный.
Но вся прелесть имхо - не в ответе, а в рассуждениях

k - это переменная для вычисления регулярной дискретной последовательности, в данном случае суммы от k равно 1 до N-1 где слагаемые - функции от этого k

[Smith]

Какова вероятность что Джо сядет на своё место?

Не, вероятность что займёт равна 1 - вероятность, что не займёт

buka, так вероятность что сядет, или что не сядет (займет/не займет)?? вы уж определитесь, плз
и как вероятность того, что джо займет свое место может быть равна 1? 
зы: запутали вы меня совсем..