|
Um_nik
Гость
|
 |
� : Март 07, 2011, 07:57:22 � |
|
1. Решить в целых числах (решено - zhekas) 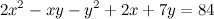 2. Решить в целых числах 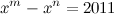 где m,n - натуральные числа 3. Решить (решено - zhekas) 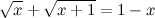 |
|
|
|
� Последнее редактирование: Март 07, 2011, 09:58:03 от Um_nik �
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #1 : Март 07, 2011, 08:45:19 � |
|
Показать скрытый текст 1. (13,14) (13,-20) (6,1) (6,0) (-24,-20) (-24,51) (-7,0) (-7,14)
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #2 : Март 07, 2011, 08:47:03 � |
|
Да, забыл добавить, надо с решениями  |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #3 : Март 07, 2011, 09:07:42 � |
|
Показать скрытый текст 1.
2x^2 - xy - y^2 + 2x + 7y -12 = 84 - 12
(x-y+3)(2x+y-4)=72=2^3*3^2
x-y+3=a
2x+y-4=b a*b=72
3x=(a+b)+1
откуда пара a,b может быть (2,36) (8,9) (-1,-72) (-4,-18) (36,2) (9,8) (-72,-1) (-18,-4)
подставляем в систему и решаем. Ответ дан выше
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #4 : Март 07, 2011, 09:09:55 � |
|
После все элементарно. Но это-то как? |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #5 : Март 07, 2011, 09:12:09 � |
|
Показать скрытый текст 3. Слева выражение >=1 справа <=1значит решение при правой и левой частях равных 1-x=1
x=0
подставляем и проверяем что x=0 корень уравнения.
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #6 : Март 07, 2011, 09:15:52 � |
|
Показать скрытый текст 3. Слева выражение >=1 справа <=1значит решение при правой и левой частях равных 1-x=1
x=0
подставляем и проверяем что x=0 корень уравнения.
Верно  Ну и остался самый легкий) |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #7 : Март 07, 2011, 09:20:10 � |
|
После все элементарно. Но это-то как?
я раскладывал квадратный трёхчлен относительно x
2x^2 - xy - y^2 + 2x + 7y
2x^2 - x(y-2) + (7y - y^2 )
найдём дискрминант
D=(y-2)^2 - 4*2*(7y-y^2) = 9y^ 2 - 60y + 4
до полного квадрата не хватает 96, тоесть в свободнос члене не трёхчлена не хватает -12
2x^2 - xy - y^2 + 2x + 7y -12 = 84 - 12
ну а теперь в левой части легко найти корни квадратного трёчлена относительно x и соответственно разложить на множители
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #8 : Март 07, 2011, 09:22:17 � |
|
После все элементарно. Но это-то как?
я раскладывал квадратный трёхчлен относительно x
2x^2 - xy - y^2 + 2x + 7y
2x^2 - x(y-2) + (7y - y^2 )
найдём дискрминант
D=(y-2)^2 - 4*2*(7y-y^2) = 9y^ 2 - 60y + 4
до полного квадрата не хватает 96, тоесть в свободнос члене не трёхчлена не хватает -12
2x^2 - xy - y^2 + 2x + 7y -12 = 84 - 12
ну а теперь в левой части легко найти корни квадратного трёчлена относительно x и соответственно разложить на множители
красиво  |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #9 : Март 07, 2011, 13:05:18 � |
|
2. Показать скрытый текст
x^a(x^b-1) = 2011
2011 простое число
поэтому либо x^a=+-1 не являются корнем
либо x^b-1=+-1 x^b=2 x=2 не является корнем x^b=0 x=0 не является корнем
Ответ: решение нет
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
семеныч
|
 |
� Ответ #10 : Март 07, 2011, 13:12:32 � |
|
разница степеней одного и того числа - число четное  |
|
|
|
|
 Записан
Записан
|
звездовод-числоблуд
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #11 : Март 07, 2011, 13:17:09 � |
|
разница степеней одного и того числа - число четное  Так-то лучше) |
|
|
|
|
 Записан
Записан
|
|
|
|
|

