1) Вычислите
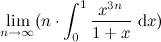
2) Докажите, что для любого натурального ненулевого числа n, число E является квадратом натурального числа:
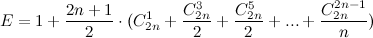
3) Пусть задана правильная четырёхугольная пирамида SABCD. Плоскость пересекает рёбра (SA), (SB), (SC), (SD) в точках M, N, P, Q соответственно. Если сумма площадей треугольников SMN и SPQ равна сумме площадей треугольников SNP и SQM, докажите , что диагонали четырёхугольника MNPQ перпендикулярны, а MN = MQ и PN = PQ.
4) Найдите все первообразные функции
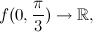
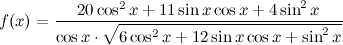
5) Вычислите определённый интеграл
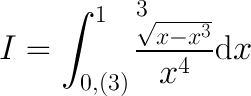
6) Пусть
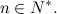
Найдите все первообразные функции
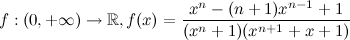
7) Основанием тетраэдра ABCD является равносторонний треугольник ABC, а точка О плоскости (АВС) является основанием высоты тетраэдра, проведённой из вершины D. Известно, что объём тетраэдра равен V и выполняются следующие соотношения :
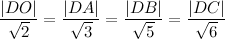
8.) Найдите площадь фигуры, ограниченной графиками функций
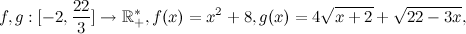
и прямыми, задающими область их определения.
9) Доказать существование и найти число, кратное числу 2011 и имеющее ровно 2011 натуральных делителей.
10) Дан куб и точка принадлежащая его внутренней области, которую соединили с двумя рядом стоящими вершинами, притом получили тупой угол
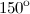
.
Докажите, что при соединении данной точки с оставшимися двумя рядом стоящими вершинами, получим равносторонний треугольник.


