Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� : Март 06, 2011, 21:07:59 � |
|
Возьмём отрезок верёвки и ножницы. Разрежем в произвольном месте на 2 отрезка. Пусть координата разреза Х0. (вещественное) Теперь какова была вероятность разрезать этот кусок верёвки именно в координате Х0? Вероятность этого события 0 Показать скрытый текст =толщина точки / длинна отрезка , но оно ведь произошло! События с вероятностью 0 происходят. Показать скрытый текст Следствие : События с вероятностью 1 могут не произойти. |
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #1 : Март 06, 2011, 21:09:04 � |
|
Не 0, а бесконечно мала
|
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #2 : Март 06, 2011, 21:10:31 � |
|
Не 0, а бесконечно мала
 я бы всётаки сказал 0Правило вычисления геометрической вероятности. Имеется некоторая область на прямой (на плоскости, в пространстве). В этой области наугад выбираются случайные точки так, что вероятность попадания точки в любую часть области пропорциональна ее длине (площади, объему) и не зависит от расположения и формы подобласти. Тогда вероятность попадания точки в область можно вычислить по одной из формул: ( L 0- длина искомого отрезка, L - длинна всего отрезка) - для случайной точки на прямой; Вероятность P=L 0/L Если L 0 имеет нулевую площадь, то вероятность попадания в L 0 равна нулю. Например, вероятность попадания на отрезок (если L-прямая) или в конкретную точку будет нулевой. P = 0/L = 0 |
|
|
|
|
ianjamesbond
Свой человек
  
 Offline Offline
Сообщений: 437
СПАСИБО
-вы поблагодарили: 54
-вас поблагодарили: 58


|
 |
� Ответ #3 : Март 06, 2011, 21:15:18 � |
|
Нет не 0, а очень мала тоесть бессконечно мала...
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #4 : Март 06, 2011, 21:15:46 � |
|
Предположим, что мы разрезали этот отрезок в какой-то точке.
Вероятность, что это событие произошло - 1
Для каждой точки вероятность равна некоему числу х (каждая точка имеет равную с другими вероятность).
Сумма всех этих вероятностей х равна 1.
Соответственно, х не равно 0.
|
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #5 : Март 06, 2011, 21:21:37 � |
|
Нет не 0, а очень мала тоесть бессконечно мала...
Нет смотрите мой 2-ой пост (подправил) Предположим, что мы разрезали этот отрезок в какой-то точке.
Вероятность, что это событие произошло - 1
Для каждой точки вероятность равна некоему числу х (каждая точка имеет равную с другими вероятность).
Сумма всех этих вероятностей х равна 1.
Соответственно, х не равно 0.
Твои рассуждения нельзя применить к бесконечному числу точек (бесконечная сумма) |
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #6 : Март 06, 2011, 21:24:44 � |
|
Твои рассуждения нельзя применить к бесконечному числу точек (бесконечная сумма)
Я тоже сначала вспомнил наши прения о размерности точек и прямых. И застопорился. Но в данном случае мы складываем вероятности, так что очень даже можно. |
|
|
|
|
 Записан
Записан
|
|
|
|
|
seamew
Гость
|
 |
� Ответ #7 : Март 06, 2011, 21:26:53 � |
|
Предположим, что мы разрезали этот отрезок в какой-то точке.
Вероятность, что это событие произошло - 1
Для каждой точки вероятность равна некоему числу х (каждая точка имеет равную с другими вероятность).
Сумма всех этих вероятностей х равна 1.
Соответственно, х не равно 0.
Твои рассуждения нельзя применить к бесконечному числу точек (бесконечная сумма) почему нельзя? лимит... |
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #8 : Март 06, 2011, 21:33:12 � |
|
бесконечная сумма 0 не обязательно 0. (не ставлю !, чтобы не подумали о факториале  ) ...
Твои рассуждения нельзя применить к бесконечному числу точек (бесконечная сумма)
почему нельзя? лимит... Их не счетно! Сумма не прокатит. |
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #9 : Март 06, 2011, 21:40:13 � |
|
Вероятность P=L0/L
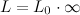 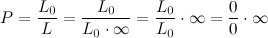 0/0 - неопределенность, однако мы можем найти эту неопределенность: Мы знаем, что сумма бесконечного числа таких вероятностей есть 1, т.е. 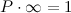 или 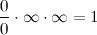 Наконец, получаем, что 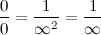 т.е. неопределенность в нашем случае "вполне определена" - это бесконечно малая величина |
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #10 : Март 06, 2011, 21:52:27 � |
|
Мой друг. L 0 - это чистый ноль. Размер точки (по определению не имеет размерности) и если с этим пунктом можно еще по философствовать (математики отдыхают), то L - вполне определённое число (например 7 сантиметров) и твоя подмена выглядит некорректно: 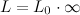 7 = 0 * беск. (хм...) Словами: заменим семёрку на ноль умноженный на бесконечность.  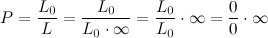 P = 0/7 = 0/(0 * беск) = 0/0 * беск далее, пардон, вообще бред: 0/0 - неопределенность, однако мы можем найти эту неопределенность: Мы знаем, что сумма бесконечного числа таких вероятностей есть 1, т.е. 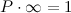 или 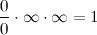 Наконец, получаем, что 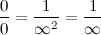 т.е. неопределенность в нашем случае "вполне определена" - это бесконечно малая величина |
|
|
|
|
|
seamew
Гость
|
 |
� Ответ #11 : Март 06, 2011, 21:58:24 � |
|
если я правильно помню, существуют правила раскрытия неопределенности...
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #12 : Март 06, 2011, 22:01:09 � |
|
Мы знаем, что в отрезке бесконечное число точек. Так что ошибки я тут не вижу.
Давно у нас "вообще бред" является математическим аргументом?
|
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #13 : Март 06, 2011, 22:07:46 � |
|
если я правильно помню, существуют правила раскрытия неопределенности...
Да. Но в отличие от другого поста, здесь НЕТ неопределённости. Ноль делённый на не нулевое число (даже беск) даёт ноль!P = L 0/L = 0/7 = 0 где вы видите неопределённость? |
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #14 : Март 06, 2011, 22:15:44 � |
|
Давно у нас "вообще бред" является математическим аргументом?
к "вообще бред" я отношу * замену конечных чисел (7) на произведение ( беск * 0) * деление обеих частей равенства на беск * исчезновение одной беск. из знаменателя 0 = 0/1 = (беск - беск)/1 = беск/1 - беск/1 = беск/1 + 0 = беск  |
|
|
|
|
|
 Голосование
Голосование

 Голосование
Голосование
