1) В треугольнике одна из медиан перпендикулярна одной из биссектрис. Найти стороны треугольника если они выражены тремя последовательными чётными числами.
2) Найти три последовательных натуральных числа, если известно что сумма цифр числа, образованного сложением кубов этих чисел, равна 27
3) Существует ли число, записанное только цифрами 3, которое делится на 93?
Задачи 1 и 2 прислал Семён Знаковян (*ALEX ALKIN*)
General
Умник
   
 Offline Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164

|
 |
� Ответ #15 : Март 12, 2010, 22:49:06 � |
|
Кстати, про число палиндром, равное сумме своих всех делителей - есть одно или два таких числа, в зависимости от формулировки. Может и больше, не знаю
|
|
|
|
|
 Записан
Записан
|
|
|
|
General
Умник
   
 Offline Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164

|
 |
� Ответ #16 : Март 13, 2010, 18:44:19 � |
|
вован, так общая формула an-1 = (100n2+20n-1)2 достаточна, или нужно что-то ещё?
|
|
|
|
|
 Записан
Записан
|
|
|
|
вован
Новенький

 Offline Offline
Сообщений: 45
СПАСИБО
-вы поблагодарили: 3
-вас поблагодарили: 5


|
 |
� Ответ #17 : Март 13, 2010, 19:36:35 � |
|
7. вот вам целый ряд квадратов чисел. что в них есть общего?
4192 9292 16392 25492 36592 49692
кто найдет?
19*20*21*22+1 = 419 229*30*31*32+1=929 239*40*41*42+1=1639 2и т.д. |
|
|
|
|
General
Умник
   
 Offline Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164

|
 |
� Ответ #18 : Март 13, 2010, 19:41:26 � |
|
красиво!
|
|
|
|
|
 Записан
Записан
|
|
|
|
вован
Новенький

 Offline Offline
Сообщений: 45
СПАСИБО
-вы поблагодарили: 3
-вас поблагодарили: 5


|
 |
� Ответ #19 : Март 13, 2010, 19:47:28 � |
|
а такая?
13=(а/в+в/с+с/а)
или
14=(а/в+в/с+с/а) 2 варианта
|
|
|
|
|
General
Умник
   
 Offline Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164

|
 |
� Ответ #20 : Март 20, 2010, 18:43:14 � |
|
Задача 11. Сумма 10-ти различных натуральных чисел равна 2010, Какое наименьшее значение может принимать сумма трёх наименьших из них? Задача 12. Решите в целых числах уравнение: 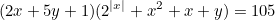 Задача 15. На столе лежат в открытую 12 карт: 4 туза (оценивается в 1 очко), 4 двойки и 4 тройки. Игроки по очереди берут карты со стола и складывают в отдельную стопку, одновременно подсчитывая количество очков в ней. Проигрывает тот, после чьего хода в стопке окажется более 21го очка. Кто выиграет при правильной игре и какова выигрышная стратегия? |
|
|
|
|
 Записан
Записан
|
|
|
|
Disciple
Новенький

 Offline Offline
Сообщений: 17
СПАСИБО
-вы поблагодарили: 2
-вас поблагодарили: 5


|
 |
� Ответ #21 : Март 21, 2010, 02:13:41 � |
|
5) В компьютерной программе хранится 5 чисел: дата (число, номер месяца) и время (часы,минуты,секунды). На ввод дается конечное выражение, состоящее из любого числа трех арифметических действий (+, -, *), скобок, 5 хранимых переменных и любых целых чисел. Выводится результат результат подсчета по формуле.
Вопрос: за какое минимальное количество запросов можно узнать, какие именно числа хранятся в программе? Привести эти запросы.
Показать скрытый текст За один. Запрос "число*100000000+месяц*1000000+час*10000+минута*100+секунда". Первые две цифры результата - это число, вторые две дата, и так далее Задача 11. Сумма 10-ти различных натуральных чисел равна 2010, Какое наименьшее значение может принимать сумма трёх наименьших из них?
Показать скрытый текст Минимальная сумма 6. (Десять чисел - 1,2,3,4,5,6,7,8,9,1965) Задача 12. Решите в целых числах уравнение: 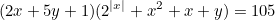 х=0, у=4. Других решений нет. |
|
|
|
|
Илья
Высший разум
    
 Offline Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...

|
 |
� Ответ #22 : Март 22, 2010, 08:52:15 � |
|
Вопрос на счет задачи №15. Как может оказаться в стопке у кого-то из игроков больше 21, если изначально было 4*2+4*3+4= 24 очка?
|
|
|
|
|
 Записан
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
Валерий
Гений-Говорун

 Offline Offline
Сообщений: 1395
СПАСИБО
-вы поблагодарили: 157
-вас поблагодарили: 235

|
 |
� Ответ #23 : Март 22, 2010, 09:16:16 � |
|
Вопрос на счет задачи №15. Как может оказаться в стопке у кого-то из игроков больше 21, если изначально было 4*2+4*3+4= 24 очка?
Они не себе их берут, а складывают в общую стопку. |
|
|
|
|
 Записан
Записан
|
|
|
|
Илья
Высший разум
    
 Offline Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...

|
 |
� Ответ #24 : Март 22, 2010, 09:18:07 � |
|
Ясно.
|
|
|
|
|
 Записан
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
Disciple
Новенький

 Offline Offline
Сообщений: 17
СПАСИБО
-вы поблагодарили: 2
-вас поблагодарили: 5


|
 |
� Ответ #25 : Март 22, 2010, 23:59:26 � |
|
Задача 15.
На столе лежат в открытую 12 карт: 4 туза (оценивается в 1 очко), 4 двойки и 4 тройки.
Игроки по очереди берут карты со стола и складывают в отдельную стопку, одновременно подсчитывая количество очков в ней. Проигрывает тот, после чьего хода в стопке окажется более 21го очка. Кто выиграет при правильной игре и какова выигрышная стратегия?
Показать скрытый текст Выигрывает первый. Для этого ему стоит вначале скидывать в стопку карты номиналом 2(двойки).
-Если он будет играть двойками только один. То на это унего уйдет 4 хода. Второй за эти четыре хода скинет 4 карты. И четыре карты остануться на столе. Возможны 5 случаев:
1)Остались карты - 3 3 3 3.
Значит сумма в стопке 12(всего сумма 24,и 12 на столе). после след круга (очередного хожа первого, а потом второго игрока) на столе остануться две тройки и сумма стопки будет 18. Перый кладет еще одну 3 в стопку. Сумма стопки 21, и второй проигрывает.
2)Остались 3 3 3 1. Первый ходит еденицей, второму приходиться ходить тройкой. остались две тройки и сумма стопки 18. Концовка аналогична 1)
3)Остались 3 3 1 1. Сумма стопки при этом 16(на столе 8 очков). Первый ходит 3. Сумма стопки 19. Если второй сходит 3,то проиграет, поэтому вынужден хотить 1. Сумма стопки 20. Первый ходит 1. Сумма стопки 21. Второй проиграл.
4)Остались 3 1 1 1. Сумма стопки 18. Первый ходит 3. Сумма втопки 21. Второй проиграл.
5)Остались 1 1 1 1. Сумма стопки 20. Первый ходит 1. сумма стопки 21. Второй проиграл.
-Если же двойки кончились раньше 4 хода первого(Двойки скидывал не только он, но и второй игрок), то первый ходит как захочет до тех пор пока на столе не останется 4 карты. А так как на столе нет двоек, то это будет одна из 5 рассмотренных выше ситуаций, в которых Первый выиграет |
|
|
|
|
General
Умник
   
 Offline Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164

|
 |
� Ответ #26 : Март 23, 2010, 23:29:49 � |
|
Поправка: в задаче 11 на самом деле нужно найти наибольшее значении суммы трёх наименьших слагаемых
Disciple,
[spoiler]Да, красиво, я сам решал по-другому, через выигрышные и проигрышные позици�
|
|
|
|
� Последнее редактирование: Март 24, 2010, 19:27:47 от General �
|
 Записан
Записан
|
|
|
|
Disciple
Новенький

 Offline Offline
Сообщений: 17
СПАСИБО
-вы поблагодарили: 2
-вас поблагодарили: 5


|
 |
� Ответ #27 : Март 24, 2010, 01:30:32 � |
|
Поправка: в задаче 11 на самом деле нужно найти наибольшее значении суммы трёх наименьших слагаемых
Показать скрытый текст Тогда ответ 591. И числа 196,197,198,199,200,201,202,203,204,210.
Пусть а1,а2,а3...а9,а10 числа, упорядоченные по возрастанию и их сумма равна 2010.
Если а1+а2+а3>=592, тогда а3>=199(если это не так и а3<199, то есть а3<=198, то а2<=197 и а1<=196, и а1+а2+а3<=591). Отсюда получаем что а4>=200,а5>=201..а10>=206.Проссумируем неравенства:
а1+а2+а3>=592
а4>=200
а5>=201
а6>=202
а7>=203
а8>=204
а9>=205
а10>=206, и получим что сумма а1+а2+..+а9+а10>=2013. Противоречие условию. Значит Сумма а1+а2+а3<592.
|
|
|
|
|
 Записан
Записан
|
|
|
|
buka
Гений
    
 Offline Offline
Сообщений: 960
СПАСИБО
-вы поблагодарили: 4
-вас поблагодарили: 120

|
 |
� Ответ #28 : Март 24, 2010, 03:53:44 � |
|
Поправка: в задаче 11 на самом деле нужно найти наибольшее значении суммы трёх наименьших слагаемых
Показать скрытый текст Тогда ответ 591. И числа 196,197,198,199,200,201,202,203,204,210.
Пусть а1,а2,а3...а9,а10 числа, упорядоченные по возрастанию и их сумма равна 2010.
Если а1+а2+а3>=592, тогда а3>=199(если это не так и а3<199, то есть а3<=198, то а2<=197 и а1<=196, и а1+а2+а3<=591). Отсюда получаем что а4>=200,а5>=201..а10>=206.Проссумируем неравенства:
а1+а2+а3>=592
а4>=200
а5>=201
а6>=202
а7>=203
а8>=204
а9>=205
а10>=206, и получим что сумма а1+а2+..+а9+а10>=2013. Противоречие условию. Значит Сумма а1+а2+а3<592.
Можно проще.
Определим верхнюю границу меньшего числа.
Чтобы 3 минимальных слагаемых из 10 разных, дающих сумму 2010 были максимальными, максимальное из них д/б минимальным, второе - на 1 меньше и т.д., короче - эти 10 слагаемых д/б последовательными 10-ю числами.
Х + Х + 1 + Х + 2 + ... + Х + 9 = 2010;
10*Х + 1 + 2 + 3 + ... + 9 = 2010.
Х = (2010 - 45)/10 = 196.5, т.е. оно дробное.
Максимальное целое тогда будет 196.
Тогда сумма 10 последовательных составит 2005, поэтому последнее нужно увеличить на 5 (...204,210 вместо ...204,205)
Можно увеличивать 2 последних числа (вместо ...204,210 -> ...205,209, или 3 последних числа и т.д., но не более 5 последних чисел.
Другими словами, эти лишние 5 нельзя "растворить" среди меньших.
Тогда сумма 3 составит 196 + 197 +198 и никак не больше... |
|
|
|
|
 Записан
Записан
|
|
|
|
sek140675
Гений-Говорун

 Offline Offline
Сообщений: 1861
СПАСИБО
-вы поблагодарили: 283
-вас поблагодарили: 108


|
 |
� Ответ #29 : Март 24, 2010, 09:01:19 � |
|
Кстати, про число палиндром, равное сумме своих всех делителей - есть одно или два таких числа, в зависимости от формулировки. Может и больше, не знаю
а можно увидеть ответ про палиндром? |
|
|
|
|
 Записан
Записан
|
|
|
|
|
