Началась
//текст доступен после регистрации//открытая Интернет-олимпиада по математике! Вас опять ожидают 7 нестандартных задач, оценивающихся по 7 баллов каждая.
Решения задач присылайте по адресу:
intelmath@narod.ru или в ЛС. Приветствуется сопровождение решения Вашими комментариями относительно интереса задачи и её сложности.
Подведение итогов олимпиады состоится во вторник, 18 мая.
Задача 1. Приближение произведениемОтношение двух наименьших трёхзначных простых чисел
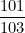
равно 0,980583…
Найдите несколько таких простых дробей с числителями и знаменателями, не превосходящими 50, произведение которых отличалось бы от
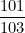
менее чем на 10
-5Задача 2. Стохастический БашеВася и Петя отлично умеют анализировать Баше-подобные игры, поэтому они решили несколько разнообразить игровой процесс.
Сначала Вася называет некоторое число 50<N<100. На стол кладётся N спичек.
Далее при помощи обычного игрального кубика (с числами от 1 до 6 на гранях) выбрасываются три числа: a, b и c (2 или 3 из них могут оказаться равными).
Игроки по очереди берут из стопки a, b или c спичек. Проигрывает тот, кто не может сделать ход.
Какое число нужно назвать Васе, чтобы максимизировать свои шансы на выигрыш, если первым будет ходить Петя?
Задача 3. Сумма рядаНайдите закономерность и вычислите сумму всех элементов последовательности
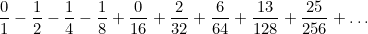Задача 4. КартыНа столе в закрытую лежат 8 карт. Известно, что там 4 красные и 4 чёрные карты. Вы выбираете из них две случайным образом. Какова вероятность того, что эти две карты окажутся одного цвета?
Задача 5. Треугольник из отрезковЕдиничный отрезок случайным образом разбивается на две части. Затем б
ольшая часть опять случайным образом разбивается на две. Какова вероятность того, что из этих трёх частей можно составить треугольник?
Задача 6. Больше всего суммНайдите четырёхзначное число, которое можно представить в виде суммы нескольких последовательных натуральных чисел наибольшим количеством способов.
Задача 7. Жук на лентеОдин конец резиновой ленты неподвижно закреплён, а за другой тянут с постоянной скоростью v. У неподвижного конца ленты находится жук, который начинает ползти вдоль неё со скоростью u. Когда жук доползёт до противоположного конца ленты, если начальная длина ленты равна L?
Удачи!!!
General
Умник
 Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
 |
� Ответ #15 : Апрель 15, 2010, 12:50:54 � |
|
Понятно что если мы имеем n равновероятных возможностей и выбираем одну, то вероятность равна 1/n. Если рендом даёт 8 знаков после запятой, то возможных вариантов выбора - от 0,00000000 до 0,99999999 - 100 000 000 и вероятность того, что точка попадёт на 0,50000000 равна 1/100000000.
А ведь множество всех точек отрезка бесконечно. Так что при выборе какого-то конкретного числа вероятность равна 0.
|
|
|
|
|
Записан
|
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #16 : Апрель 15, 2010, 14:16:17 � |
|
Теоретически, да, число точек на отрезке бесконечно. Но если говорить о практическом разбиении отрезка, то... Вряд ли можно практически назвать разными отрезки, полученные разбиением такими двумя точками: 0,500003 и 0,500005. Согласны? Практически в обоих случаях этот будут одинаковые отрезки, хотя теоретически левая часть будет больше правой части. Впрочем, не будем дальше спорить и углубляться в дебри теории вероятностей. Будем считать, что двух равных отрезков при случайном разбиении не получается никогда (вероятность равна 0).  |
|
|
|
|
Записан
|
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #17 : Апрель 17, 2010, 16:27:14 � |
|
Ну и задали вы, General, в этот раз олимпиаду Две задачи на теорию вероятностей, сумма ряда, ещё... сами знаете что... А меня вот всегда интересовал вопрос, как можно найти сумму членов бесконечного ряда? И в университете я это так и не поняла до конца, а, может, и поняла, да сейчас снова забыла Вот, например, есть бесконечно убывающая геометрическая прогрессия (это и школьники знают): 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... Знаменатель прогрессии равен 1/2. Есть очень простая формула для суммы членов бесконечно убывающей геометрической прогрессии, по которой запросто можно вычислить сумму членов приведённой прогрессии. Но как же можно посчитать сумму всех членов, если их бесконечно много? Ну, вот 1000 членов сложили, а есть ведь ещё 1001-ый; миллион членов сложили, а есть ведь ещё миллион-первый. И так конца нет у последовательности. Как же можно сумму найти, если членов бесконечно много?  Не объясните ли, General? В вашей задаче тоже ведь надо найти сумму членов бесконечной последовательности. Так? Помню, что в универе это были ряды (да и у вас написано "сумма ряда"). Были там сходящиеся и расходящиеся ряды... Ну и всё такое прочее. |
|
|
|
� Последнее редактирование: Апрель 17, 2010, 16:30:10 от square �
|
Записан
|
|
|
|
General
Умник
Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
|
� Ответ #18 : Апрель 17, 2010, 16:45:39 � |
|
К примеру, к сумме 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... можно приёти так. сначала предположим, что ряд обрывается на некотором слагаемом 1/2^k. Тогда прибавив ещё 1/2^k к этому ряду, он свернётся в единицу. Значит, сумма 1/2+...+1/2^k равна 1-1/2^k. Ну а с увеличением количества слагаемых она будет всё меньше отличаться от единицы. Вот я так это понимаю. Кстати, я недавно писал о //текст доступен после регистрации//, вгляните |
|
|
|
|
Записан
|
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #19 : Апрель 17, 2010, 16:53:38 � |
|
Нет, ничего не поняла  Как бы ни были малы следующие члены, но они всё же есть и их нельзя совсем отбросить. Они всё равно сумму буду изменять. Я помотрела по указанной ссылке ваш метод "свёртывания" двух рядом стоящих дробей. Но у вас там было конечное число членов, а не бесконечное ! |
|
|
|
� Последнее редактирование: Апрель 17, 2010, 16:59:28 от square �
|
Записан
|
|
|
|
General
Умник
Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
|
� Ответ #20 : Апрель 17, 2010, 17:15:36 � |
|
Нутак сначала доказываем для конечного количества, что сумма будет меньше единицы на 1/2^k.
Если добавлять слагаемые, их количество k ,eltn увеличиваться, а разница с единицей - уменьшаться. Значит, для бесконечного количества слагаемых сумма будет равна единице.
|
|
|
|
|
Записан
|
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #21 : Апрель 17, 2010, 17:24:01 � |
|
Ну, что-то мне вспоминается из теории сходимости рядов. Сумма сходящегося ряда вроде бы определялась через некий предел. Правильно?
Вы сейчас пытаетесь объяснить "на пальцах". А строго это надо объяснять через предел вот этой самой величины 1/2^k при k стремящемся к бесконечности. И предел этот будет равен нулю. Вот как-то так.
Но изучают ли в школе теорию рядов? А диф. уравнения?
Или вы в своей олимпиаде на школьников не рассчитываете?
|
|
|
|
|
Записан
|
|
|
|
General
Умник
Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
|
� Ответ #22 : Апрель 17, 2010, 17:38:33 � |
|
И на школьников расчитываю. И изучают всё это.
|
|
|
|
|
Записан
|
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #23 : Апрель 17, 2010, 17:54:50 � |
|
Да-а-а, продвинутые нынче стали школьники  Я уж, пожалуй, теперь с ними не смогу соревноваться со своим забытым университетским образованием |
|
|
|
|
Записан
|
|
|
|
General
Умник
Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
|
� Ответ #24 : Апрель 17, 2010, 18:00:16 � |
|
В углублённых, по крайней мере, затрагивают.
А олимпиаду я для всех желающих провожу
|
|
|
|
|
Записан
|
|
|
|
Семён
Свой человек
Offline
Сообщений: 335
СПАСИБО
-вы поблагодарили: 81
-вас поблагодарили: 32
ᵀ ᴴ ᴱ ᴼ ᴿ ᴵ ᴳ ᴵ ᴻ ᴬ ᴸ
|
|
� Ответ #25 : Апрель 17, 2010, 18:07:15 � |
|
похоже изучают,но не все...тип образования вовсе не слишком меняется...в разных государствах-разные требования..
Вот у нас- в Молдавии- всё выше предложеное-строки заумных писателей,теории гениев своего дела)..
Но всё же,обижаться не будем..ведь что нынче не ко благу,то на будующее - к добру..А за олимпиаду-спасибоогромное..хотя прошлая-интересней была!
Но,всякий труд ценен,тем более- авторство!
|
|
|
|
|
Записан
|
Скайп: Skype_awerty777
Ок: ok.ru/exclusion
VK: vk.com/exclusi0n
|
|
|
square
Свой человек
Offline
Сообщений: 333
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 14
|
|
� Ответ #26 : Апрель 17, 2010, 18:15:43 � |
|
Да, я понимаю, что для всех желающих. Но это, наверное, не совсем правильная тактика. Потому что всё-таки школьники не могут в полной мере знать ту теорию, которую затрагивают ваши задачи. Мне пишет один школьник в личку. Так вот, он говорит, что теорию вероятностей они как-то игнорируют, то есть не изучают, так я поняла. А у вас две задачи на теорию вероятностей. При этом одна из них элементарная для тех, кто эту теорию знает хотя бы чуть чуть. А кто совсем понятия не имеет, для тех и эта задача сложная. О задаче про жука на ленте я вам уже всё сказала. Во-первых, она всё-таки больше физическая, чем математическая. Ну, и такое сложное решение - это тоже, как мне кажется, школьники не потянут. Поэтому олимпиады, на мой взгляд, надо всё-таки проводить более адресно. Есть олимпиады для школьников, есть для студентов. Ну, если для всех желающих, тогда, конечно, все могут решать. Да только вот школьники-то тоже желающие А по письмам одного из них я вижу, что ему эти задачи не очень поддаются. Ни теорию рядов, ни теорию вероятностей, ни диф. уравнения он, судя по всему, не знает. |
|
|
|
|
Записан
|
|
|
|
General
Умник
Offline
Сообщений: 681
СПАСИБО
-вы поблагодарили: 47
-вас поблагодарили: 164
|
|
� Ответ #27 : Апрель 17, 2010, 18:31:41 � |
|
Дело в том, что почти ко всем этим задачам можно подойти элементарными методами. И, во-вторых, отчасти поэтому я выделяю на олимпиаду месяц.
|
|
|
|
|
Записан
|
|
|
|
Семён
Свой человек
Offline
Сообщений: 335
СПАСИБО
-вы поблагодарили: 81
-вас поблагодарили: 32
ᵀ ᴴ ᴱ ᴼ ᴿ ᴵ ᴳ ᴵ ᴻ ᴬ ᴸ
|
|
� Ответ #28 : Апрель 17, 2010, 20:50:49 � |
|
Все правы по своему,но МиР - дороже всего!!!
|
|
|
|
|
Записан
|
Скайп: Skype_awerty777
Ок: ok.ru/exclusion
VK: vk.com/exclusi0n
|
|
|
sek140675
Гений-Говорун
Offline
Сообщений: 1861
СПАСИБО
-вы поблагодарили: 283
-вас поблагодарили: 108
|
|
� Ответ #29 : Апрель 21, 2010, 08:31:28 � |
|
К примеру, к сумме 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... можно приёти так. сначала предположим, что ряд обрывается на некотором слагаемом 1/2^k. Тогда прибавив ещё 1/2^k к этому ряду, он свернётся в единицу. Значит, сумма 1/2+...+1/2^k равна 1-1/2^k. Ну а с увеличением количества слагаемых она будет всё меньше отличаться от единицы. Вот я так это понимаю. Кстати, я недавно писал о //текст доступен после регистрации//, вгляните Найдите значения бесконечного произведения //текст доступен после регистрации// |
|
|
|
|
Записан
|
|
|
|
|
