Пусть в некотором царстве, в некотором государстве принцесса решила, что ей пора найти себе жениха. Созвали царевичей и королевичей со всего света, и явилось 1000 претендентов. Про любых двух когда-либо
увиденных принцесса может сказать, кто из них лучше. При этом царевичи, как говорят математики, образуют упорядоченное множество, т. е. если Иван Царевич лучше Василия Царевича, а Василий Царевич лучше Фёдора Царевича, то Иван Царевич лучше Фёдора Царевича. Претенденты входят к принцессе по очереди, по одному, причём их порядок определён случайным образом, т. е. вероятность появления какого-то царевича первым, или пятисотым, или тысячным совершенно одинакова. Принцесса, разумеется, умея их сравнивать, может сказать, что, например, вошедший тридцатым является десятым по качеству, т. е. девять из предыдущих были лучше, а остальные — хуже, и т. д. Цель принцессы — получить самого хорошего жениха, т. е. даже второй её не устраи-
вает. На каждом шаге, т. е. после встречи с каждым из царевичей, она решает, берёт ли она его в мужья. Если берёт, то на этом смотр претендентов заканчивается, они все разъезжаются по домам. Если же принцесса ему отказывает, то царевич, будучи отвергнутым, тут же уезжает домой, потому что все царевичи и королевичи — люди гордые. Показ претендентов на замужество при этом продолжается. Если в конце концов принцесса не получает лучшего, то считается, что она проиграла, выходить замуж вообще не будет, а уйдёт в монастырь. Спрашивается, как действовать принцессе, чтобы с наибольшей вероятностью получить лучшего жениха. И какова эта вероятность?
P.S. Это вам не со взбалмошной старушкой и бедолагой Джо разбираться. И не кубики бросать.
Тиана
Высший разум
 Offline
Сообщений: 7313
СПАСИБО
-вы поблагодарили: 821
-вас поблагодарили: 1784
|
 |
� Ответ #15 : Февраль 02, 2011, 13:28:23 � |
|
самый лучший Царевич может и первым зайти   |
|
|
|
|
Записан
|
|
|
|
|
seamew
Гость
|
|
� Ответ #16 : Февраль 02, 2011, 14:08:13 � |
|
самый лучший Царевич может и первым зайти не может! пока хотя бы несколько других для сравнения не увидела, он не "лучший", а "первый встречный" |
|
|
|
|
Записан
|
|
|
|
|
Um_nik
Гость
|
|
� Ответ #17 : Февраль 02, 2011, 14:12:01 � |
|
Ну развели флудилку)) Задачка-то интересная, хотя и сложная  |
|
|
|
|
Записан
|
|
|
|
Тиана
Высший разум
Offline
Сообщений: 7313
СПАСИБО
-вы поблагодарили: 821
-вас поблагодарили: 1784
|
|
� Ответ #18 : Февраль 02, 2011, 14:21:59 � |
|
не может! пока хотя бы несколько других для сравнения не увидела, он не "лучший", а "первый встречный"
как не может? вероятность появления каждого царевича одинаковая зы: так что "любовь с первого раза взгляда" вполне возможна  |
|
|
|
|
Записан
|
|
|
|
|
Um_nik
Гость
|
|
� Ответ #19 : Февраль 02, 2011, 15:24:31 � |
|
Я не помню, как решать, поэтому попробую сам: Показать скрытый текст Нам нужно пропустить N женихов, а потом выбрать первого, который был бы лучше первых N. Вот формула вероятности успеха: 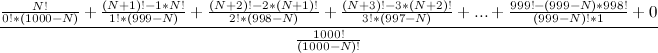 Осталось только как-то найти ее максимум |
|
|
|
|
Записан
|
|
|
|
|
seamew
Гость
|
|
� Ответ #20 : Февраль 02, 2011, 15:44:22 � |
|
может, продиффиринцировать?
|
|
|
|
|
Записан
|
|
|
|
|
Um_nik
Гость
|
|
� Ответ #21 : Февраль 02, 2011, 15:47:14 � |
|
может, продиффиринцировать?
Та да, но я не знаю, как такие функции дифференцировать. |
|
|
|
|
Записан
|
|
|
|
|
seamew
Гость
|
|
� Ответ #22 : Февраль 02, 2011, 16:09:37 � |
|
нам надо узнать, при каком N эта твоя жуткая формула имеет максимальное значение... нужно ее примерно построить и посмотреть, где максимум...
|
|
|
|
|
Записан
|
|
|
|
Вилли ☂
Гений-Говорун
Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃
|
|
� Ответ #23 : Февраль 02, 2011, 16:40:24 � |
|
А мне это напомнило задачу о двух конвертах.
Мы выбираем конверт (мы не знаем, что там) == К нам заходит прынц (мы еше не знаем какой он)
Мы смотрим содержимое (оцениваем, узнаём) == Мы оцениваем прынца узнаём его "вес"
Нам предлагают поменят' конверт == Нам предлагают поменят' принца (сказат' нет и смотрет' следуюшего)
"Мощность" ("хорошеть") принцев как и сумм в конвертах вполне ограниченное число.
Мы стоим перед выбором: поменят' этого принца (этот конверт) на другого, в надежде получит' лучший вариант
|
|
|
|
� Последнее редактирование: Февраль 02, 2011, 16:42:05 от Вилли �
|
Записан
|
|
|
|
|
seamew
Гость
|
|
� Ответ #24 : Февраль 02, 2011, 16:42:26 � |
|
А мне это напомнило задачу о двух конвертах.
Мы выбираем конверт == К нам заходит прынц
Мы смотрим содержимое (оцениваем) == Мы оцениваем прынца
Нам предлогают поменят' конверт == Нам предлогают поменят' принца (сказат' нет и смотрет' следуюшего)
"Мощность" ("хорошест'") принцев как и сумм в конвертах вполне ограниченное число.
Мы стоим перед выбором: поменят' этого принца (этот конверт) на другого, в надежде получит' лучший вариант
не, тут фишка-то получить не лучший, а Наилучший вариант. Или не получить ничего... |
|
|
|
|
Записан
|
|
|
|
VVV
Умник
Offline
Сообщений: 662
СПАСИБО
-вы поблагодарили: 20
-вас поблагодарили: 55
|
|
� Ответ #25 : Февраль 02, 2011, 16:43:34 � |
|
Как верно заметил Um_nik, если принцесса не угадала, то она уходит в монастырь. Нелегка жизнь принцессы. У нее нет стратегии , которая гарантирует 100% успех.
Можно заметить, что любая разумная стратегия принцессы сводится к выбору числа. Но мудро выбрать число сложно. Дерзайте!
|
|
|
|
|
Записан
|
Правила и тактика игры в "ассоциации". //текст доступен после регистрации// . Дополнительные методы, архив партий //текст доступен после регистрации// . |
|
|
Вилли ☂
Гений-Говорун
Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃
|
|
� Ответ #26 : Февраль 02, 2011, 16:46:52 � |
|
Ну хорошо. Метод: "Закрыт' глаза и выбрат' наугад" Вероятност': 1/1000 Следовател'но, если ест' лучший метод, то он должен дат' бол'шую вероятност'  @Um_nik: Откуда формула? |
|
|
|
|
Записан
|
|
|
|
Илья
Высший разум
Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...
|
|
� Ответ #27 : Февраль 02, 2011, 16:47:44 � |
|
|
|
|
|
|
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
|
seamew
Гость
|
|
� Ответ #28 : Февраль 02, 2011, 16:51:08 � |
|
Принцесса, разумеется, умея их сравнивать, может сказать, что, например, вошедший тридцатым является десятым по качеству, т. е. девять из предыдущих были лучше, а остальные — хуже, и т. д.
смотрите, если она отсмотрела N претендентов, cледующим входит обалденный красавчик N+1, который лучше всех!! предыдущих, то ей надо выбирать его.
Т.к. выбрав принца N+1:
1. она точно получает лучшего из всех просмотренных
2. она его оставляет, то есть остальных она не смотрит (не может же она выбранного прогнать). следовательно из всех (виденных), она выбрала лучшего...
|
|
|
|
|
Записан
|
|
|
|
|
Um_nik
Гость
|
|
� Ответ #29 : Февраль 02, 2011, 16:54:05 � |
|
@Um_nik: Откуда формула?
Начиркал) |
|
|
|
|
Записан
|
|
|
|
|
