greggreen
Новенький

 Offline Offline
Сообщений: 3
СПАСИБО
-вы поблагодарили: 1
-вас поблагодарили: 0


|
 |
� : Март 22, 2011, 13:07:43 � |
|
x*a+((c+1/x*b)*(d*e))/(c+d+e+1/x*b) =0
привисти к виду квадратного уравнения по x (x^2....+x....+)
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #1 : Март 22, 2011, 13:14:18 � |
|
Интересно, откуда тут взяться квадратному уравнению? 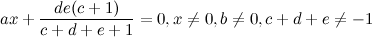 |
|
|
|
|
 Записан
Записан
|
|
|
|
greggreen
Новенький

 Offline Offline
Сообщений: 3
СПАСИБО
-вы поблагодарили: 1
-вас поблагодарили: 0


|
 |
� Ответ #2 : Март 22, 2011, 13:21:11 � |
|
Повторяю, задача состоит в приведении данного выражения к квадратному уравнению. x*a+((c+1/x*b)*(d*e))/(c+d+e+1/x*b) =0
привисти к виду квадратного уравнения по x (x^2....+x....+)
|
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #3 : Март 22, 2011, 13:23:37 � |
|
Ну если очен' хочется, то
А * x^2 + B * x + C = 0
где
А = а2
B = 0
C = -( (cde + de)/(c + d + e + 1) )2
т.е.
а2*х2 - ( (cde + de)/(c + d + e + 1) )2 = 0
|
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #4 : Март 22, 2011, 13:24:26 � |
|
Во-первых, воспользуйтесь //текст доступен после регистрации// , т.к. возможно, что Вы просто неправильно написали условие. Во-вторых, если я дам задание уравнение х=4 сделать квадратным, то оно невыполнимо. |
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #5 : Март 22, 2011, 13:25:33 � |
|
Во-первых, воспользуйтесь //текст доступен после регистрации// , т.к. возможно, что Вы просто неправильно написали условие. Во-вторых, если я дам задание уравнение х=4 сделать квадратным, то оно невыполнимо. х = 4 х 2 = 16  |
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #6 : Март 22, 2011, 13:25:37 � |
|
Вилли, эти уравнения не равносильны, могут получиться посторонние корни
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #7 : Март 22, 2011, 13:26:37 � |
|
Во-первых, воспользуйтесь //текст доступен после регистрации// , т.к. возможно, что Вы просто неправильно написали условие. Во-вторых, если я дам задание уравнение х=4 сделать квадратным, то оно невыполнимо. х = 4 х 2 = 16  Решаем первое: х=4 Решаем второе: х=4, х=-4. Уравнения не равносильны, замена неправомерна |
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #8 : Март 22, 2011, 13:33:40 � |
|
Вилли, эти уравнения не равносильны
А я это и не утверждал. х = 4 х 2 = 16  Решаем первое: х=4 Решаем второе: х=4, х=-4. Уравнения не равносильны, замена неправомерна Из первого уравнения можно перейти ко второму без потер'. Все корни первого сохраняются корнями и для второго. Мы не домножаем/делим на 0 А вот от второго к первому переход без потер' не возможен. Это верно. Итак: х=4 -> х 2=16  Из первого следует второе. но х2=16 -> х=4  |
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #9 : Март 22, 2011, 13:44:54 � |
|
Нужно привести к виду, т.е. заменить равносильным
|
|
|
|
|
 Записан
Записан
|
|
|
|
Вилли ☂
Гений-Говорун

 Offline Offline
Сообщений: 1572
СПАСИБО
-вы поблагодарили: 532
-вас поблагодарили: 722
☃

|
 |
� Ответ #10 : Март 22, 2011, 13:59:50 � |
|
А * x^2 + B * x + C = 0 где А = 0
B = a
C = (cde + de)/(c + d + e + 1)т.е. |
|
|
|
|
 Записан
Записан
|
|
|
|
|
Um_nik
Гость
|
 |
� Ответ #11 : Март 22, 2011, 14:04:25 � |
|
Вообще да, я это и хотел написать сначала. Но нас учат, что Квадратное уравнение, это уравнение вида 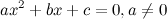 |
|
|
|
|
 Записан
Записан
|
|
|
|
|

