В школе начался ремонт и контрольную работу провели в актовом зале для всех классов.
Для каждого класса была написаны следующие задачи:
7 класс
Найдите нечетное натуральное число, не превосходящее 1000, если известно, что сумма последних цифр всех его делителей (включая 1 и само число) равна 33.
8 класс
Вычислите число √5,44…4 (после запятой следует 100 четверок) с точностью до 10⁻¹⁰⁰.
9 класс
На окружности отмечено 16 точек. Найдите наибольшее возможное число остроугольных треугольников, с вершинами в отмеченных точках.
Tmin
Свой человек
 Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
 |
� Ответ #60 : Сентябрь 17, 2015, 03:27:58 � |
|
Я могу доказать, что максимум 168. Я оценивал, наоборот, минимум неостроугольных и получил 39 2. А всего 560.
ответ верный, доказательство отличное. Аплодисменты!!!  Актовый зал закрываем.. |
|
|
|
|
Записан
|
|
|
|
Бляхамуха
Свой человек
Offline
Сообщений: 345
СПАСИБО
-вы поблагодарили: 138
-вас поблагодарили: 81
|
|
� Ответ #61 : Сентябрь 17, 2015, 07:03:27 � |
|
Я, да, ошиблась с градусами, остроугольных треугольников много меньше.
Может под занавес отобразите графически распределение точек на окружности и кол-во треугольников из одной точки?
|
|
|
|
|
Записан
|
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #62 : Сентябрь 17, 2015, 07:32:27 � |
|
Я, да, ошиблась с градусами, остроугольных треугольников много меньше.
Может под занавес отобразите графически распределение точек на окружности и кол-во треугольников из одной точки?
распределение точек на окружности не имеет значения (см. Условие задачи)  |
|
|
|
|
Записан
|
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #63 : Сентябрь 17, 2015, 07:39:22 � |
|
Могу спросить: каково наибольшее число остроугольных треугольников, если на окружности отмечены 32 точки. Пример доказательства уже есть.  |
|
|
|
|
Записан
|
|
|
|
v-lad
Гений-Говорун
Offline
Сообщений: 1002
СПАСИБО
-вы поблагодарили: 530
-вас поблагодарили: 258
|
|
� Ответ #64 : Сентябрь 17, 2015, 07:42:46 � |
|
имеет значение!
ещё как имеет!!:
относительно диаметра, проходящего через первую, остальные 15 должны быть расставлены так, чтоб с одной стороны было 8, а с другой 7.
|
|
|
|
|
Записан
|
SATYAT NASTI PARO DHARMAH
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #65 : Сентябрь 17, 2015, 07:49:19 � |
|
имеет значение!
ещё как имеет!!:
относительно диаметра, проходящего через первую, остальные 15 должны быть расставлены так, чтоб с одной стороны было 8, а с другой 7.
А, докажи! Можно и графически показать, интересно. |
|
|
|
� Последнее редактирование: Сентябрь 17, 2015, 07:53:12 от Tmin �
|
Записан
|
|
|
|
zhekas
Гений-Говорун
Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487
|
|
� Ответ #66 : Сентябрь 17, 2015, 09:03:56 � |
|
Могу спросить: каково наибольшее число остроугольных треугольников, если на окружности отмечены 32 точки. Пример доказательства уже есть. Ну по логике:  |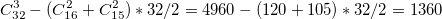
|
|
|
|
zhekas
Гений-Говорун
Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487
|
|
� Ответ #67 : Сентябрь 17, 2015, 10:05:47 � |
|
Я, да, ошиблась с градусами, остроугольных треугольников много меньше.
Может под занавес отобразите графически распределение точек на окружности и кол-во треугольников из одной точки?
распределение точек на окружности не имеет значения (см. Условие задачи) Ну что значит не важно. Если расположить все 16 точек на одной полуокружности, то все треугольники будут тупоугольными. |
|
|
|
|
Записан
|
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #68 : Сентябрь 17, 2015, 10:31:05 � |
|
Я, да, ошиблась с градусами, остроугольных треугольников много меньше.
Может под занавес отобразите графически распределение точек на окружности и кол-во треугольников из одной точки?
распределение точек на окружности не имеет значения (см. Условие задачи) Ну что значит не важно. Если расположить все 16 точек на одной полуокружности, то все треугольники будут тупоугольными. Zhekas, ты не не прав! |
|
|
|
� Последнее редактирование: Сентябрь 17, 2015, 10:35:07 от Tmin �
|
Записан
|
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #69 : Сентябрь 17, 2015, 10:38:39 � |
|
Могу спросить: каково наибольшее число остроугольных треугольников, если на окружности отмечены 32 точки. Пример доказательства уже есть. Ну по логике: C^3_32 -(C^2_16 + C^2_15)*32/2 = 4960 - (120+105)*32/2 = 1360 Сама ещё не посчитала. Придётся долго подождать. |
|
|
|
|
Записан
|
|
|
|
v-lad
Гений-Говорун
Offline
Сообщений: 1002
СПАСИБО
-вы поблагодарили: 530
-вас поблагодарили: 258
|
|
� Ответ #70 : Сентябрь 17, 2015, 11:34:08 � |
|
Ну что значит не важно. Если расположить все 16 точек на одной полуокружности, то все треугольники будут тупоугольными.
Zhekas, ты не не прав!  Тмин, если ты отметишь три точки на окружности, и сможешь провести такОй диаметр, который все три точки "бросает" в однУ половину, то треугольник стопро тупоугольный!!!  Попробуй в окружности проведи диаметр, затем на одной из полуокружностей отметь несколько точек, если найдёшь хотя бы один остроугольный треугольник, образованный этими точками, то с меня Very Superior Old Pale   |
|
|
|
|
Записан
|
SATYAT NASTI PARO DHARMAH
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #71 : Сентябрь 17, 2015, 13:14:40 � |
|
Vladu: 1. Про 3 точки даже и спорить не буду. Я противного не утверждала. 2. Zhekas утверждает, что, если расположить все 16 точек на одной полуокружности, то все треугольники будут тупоугольными. Я не согласна. 3. Твой последний пост противоречит предыдущему: "относительно диаметра, проходящего через первую, остальные 15 должны быть расставлены так, чтоб с одной стороны было 8, а с другой 7." ЗЫ. Выпей сам, я крепкие напитки не люблю. |
|
|
|
|
Записан
|
|
|
|
v-lad
Гений-Говорун
Offline
Сообщений: 1002
СПАСИБО
-вы поблагодарили: 530
-вас поблагодарили: 258
|
|
� Ответ #72 : Сентябрь 17, 2015, 13:39:49 � |
|
...
2. Zhekas утверждает, что, если расположить все 16 точек на одной полуокружности, то все треугольники будут тупоугольными. Я не согласна.
...
 Если 16 синеньких точек пронумеруешь по часовой стрелке (с низу вверх) №1,№2,...,№16, то покажи нам с Жекасом, какие Именно три образуют треугольник со всеми тремя углами, меньшыми 90 о. |
|
|
|
|
Записан
|
SATYAT NASTI PARO DHARMAH
|
|
|
v-lad
Гений-Говорун
Offline
Сообщений: 1002
СПАСИБО
-вы поблагодарили: 530
-вас поблагодарили: 258
|
|
� Ответ #73 : Сентябрь 17, 2015, 13:41:24 � |
|
...
3. Твой последний пост противоречит предыдущему: "относительно диаметра, проходящего через первую, остальные 15 должны быть расставлены так, чтоб с одной стороны было 8, а с другой 7."
...
что Именно в этом посте противоречит? |
|
|
|
|
Записан
|
SATYAT NASTI PARO DHARMAH
|
|
|
Tmin
Свой человек
Offline
Сообщений: 291
СПАСИБО
-вы поблагодарили: 22
-вас поблагодарили: 32
|
|
� Ответ #74 : Сентябрь 17, 2015, 13:57:02 � |
|
Vlad и Zhekas победили! Виноватая я!  |
|
|
|
|
Записан
|
|
|
|
|
