В тюрьме находятся 100 заключённых, и король - любитель головоломок, решил помиловать их всех, если они выполнят одно задание.
В зале на длинном столе стоят 100 одинаковых коробок, выстроенных в ряд. В каждой из
них находится уникальное имя одного из 100 узников - причём имя каждого
из них находится в одной из этих коробок. Заключенных поочередно запускают в
зал. Каждый из них имеет право открыть одну за другой 50 коробок из ста.
Если хотя бы один из них не найдёт своего имени, все они будут казнены;
если же каждому удастся найти своё имя - всех выпустят на свободу.
Узники не имеют права и возможности общаться друг с другом после
выхода из комнаты; никаких пометок в комнате делать нельзя;
перекладывать имена в коробках нельзя. Вообщем, каждый узник находит комнату в
точно том же состоянии, что и предыдущий. Единственная возможность
пообщаться - ДО испытания.
Придумайте стратегию, при которой вероятность выжить у узников будет максимальной. Какова эта вероятность?
VVV
Умник
   
 Offline Offline
Сообщений: 662
СПАСИБО
-вы поблагодарили: 20
-вас поблагодарили: 55


|
 |
� Ответ #15 : Апрель 07, 2011, 10:40:37 � |
|
Найти эту вероятность нетрудно. 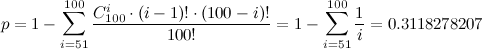 |
Правила и тактика игры в "ассоциации". //текст доступен после регистрации// . Дополнительные методы, архив партий //текст доступен после регистрации// . |
|
|
Ленка Фоменка
Сплошной мозг
  
 Offline Offline
Сообщений: 3459
СПАСИБО
-вы поблагодарили: 911
-вас поблагодарили: 689

|
 |
� Ответ #16 : Апрель 07, 2011, 10:45:51 � |
|
|
|
|
|
|
 Записан
Записан
|
Всё временно: Любовь, искусство, планета Земля, Вы, Я... Особенно Я!
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #17 : Апрель 07, 2011, 10:54:05 � |
|
Найдём вероятность что в перестановке есть цикл длиной k>50. Посчитаем их количество для этого выберем k элементов. Это можно сделать C_100^k=100!/(k!*(100-k)!) способами. Дальше расставим эти k элементов в цикле их можно расставить (k-1)! способами ну и оставшиес (100-k) элементов расставляются (100-k)! способами. Итого количество таких перестановок (100!/(k!*(100-k)!))*(k-1)!*(100-k)!=100!/k тогда вероятность цикла длины k равна (100!/k)/100!=1/k и осталось просуммировать по всем k>50 и вычесть из 1 |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #18 : Апрель 07, 2011, 14:16:34 � |
|
Интересно что при любом, даже достаточно большом количестве заключённых
у них всегда есть шанс больше 30% на выживание
|
|
|
|
|
 Записан
Записан
|
|
|
|
Илья
Высший разум
    
 Offline Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...

|
 |
� Ответ #19 : Апрель 07, 2011, 21:07:22 � |
|
Разобрались!  |
|
|
|
|
 Записан
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
BIVES
Умник
   
 Offline Offline
Сообщений: 687
СПАСИБО
-вы поблагодарили: 53
-вас поблагодарили: 272

|
 |
� Ответ #20 : Апрель 07, 2011, 21:13:13 � |
|
А как доказать, что нет лучшей стратегии?
|
|
|
|
|
 Записан
Записан
|
|
|
|
BIVES
Умник
   
 Offline Offline
Сообщений: 687
СПАСИБО
-вы поблагодарили: 53
-вас поблагодарили: 272

|
 |
� Ответ #21 : Апрель 07, 2011, 21:38:32 � |
|
Интересно что при любом, даже достаточно большом количестве заключённых
у них всегда есть шанс больше 30% на выживание Более того, если n стремится к бесконечности, а открывать можно n/2 конвертов, то вероятность будет стремится к 1. |
|
|
|
|
 Записан
Записан
|
|
|
|
zhekas
Гений-Говорун

 Offline Offline
Сообщений: 1035
СПАСИБО
-вы поблагодарили: 34
-вас поблагодарили: 487


|
 |
� Ответ #22 : Апрель 07, 2011, 22:35:19 � |
|
Интересно что при любом, даже достаточно большом количестве заключённых
у них всегда есть шанс больше 30% на выживание Более того, если n стремится к бесконечности, а открывать можно n/2 конвертов, то вероятность будет стремится к 1. нет не будет. С ростом n она вероятность будет уменьшаться а предел равен 1-ln2 |
|
|
|
|
 Записан
Записан
|
|
|
|
VVV
Умник
   
 Offline Offline
Сообщений: 662
СПАСИБО
-вы поблагодарили: 20
-вас поблагодарили: 55


|
 |
� Ответ #23 : Апрель 08, 2011, 11:54:15 � |
|
Безусловно, нужно доказать оптимальность стратегии. А в условии стоило более четко отметить, что выбираются ящики по очереди.
Задачу можно немного видоизменить. Есть, допустим, адвокат, который непосредственно перед испытанием может выбрать пару ящиков, предварительно посмотрев содержимое всех ящиков, а затем поменять местами их содержимое. В этом случае оптимальная стратегия позволяет освободиться со 100-процентной вероятностью. Если же заключенным разрешено открывать лишь треть ящиков с округлением в большую сторону, то адвокату разрешено сделать до двух обменов. Тогда снова оптимальная стратегия позволяет освободиться со 100-процентной вероятностью.
|
|
|
|
|
 Записан
Записан
|
Правила и тактика игры в "ассоциации". //текст доступен после регистрации// . Дополнительные методы, архив партий //текст доступен после регистрации// . |
|
|
Илья
Высший разум
    
 Offline Offline
Сообщений: 7695
СПАСИБО
-вы поблагодарили: 520
-вас поблагодарили: 1030
Терпение, мой друг, терпение...

|
 |
� Ответ #24 : Апрель 09, 2011, 16:29:37 � |
|
А в условии стоило более четко отметить, что выбираются ящики по очереди. Куда уж более четче: Каждый из них имеет право открыть одну за другой 50 коробок из ста.  |
|
|
|
|
 Записан
Записан
|
Рост воровства у нас неудержим,
И мы кривою роста дорожим:
Раз все воруют, значит, все при деле!
На этом-то и держится режим!
|
|
|
moonlight
Умник
   
 Offline Offline
Сообщений: 741
СПАСИБО
-вы поблагодарили: 19
-вас поблагодарили: 232


|
 |
� Ответ #25 : Июль 08, 2011, 17:11:56 � |
|
Допустим что узники ни о какой стратегии не договариваются а открывают коробки наугад. В этом случае вероятность для каждого открыть нужную коробку 50/100=1/2. Вероятность того что все 100 узников откроют коробки со своим именем (1/2) 100 или около 0.8*10 -30. Теперь пусть узникам будет позволено в случае угадывания своей коробки оставлять эту коробку открытой. В этом случае вероятность всем угадать свои коробки будет (50/100)*(50/99)*...*(50/51)=50 50*50!/100! или меньше чем 3*10 -9 и это верхний предел для любой стратегии. Оптимальная стратегия здесь была указана и состоит в том что 50 узников открывают 50 любых коробок(все одни и те же) а остальные 50 узников те коробки которые не открывались первыми. Не знаю легко ли это доказать но экспериментально это вполне подтверждается. В этом случае вероятность равна (50!) 2/100! или 10 -29. И эта формула тоже здесь была. По сравнению со случайным выбором вероятность выросла более чем в 10 раз но все равно несколько меньше чем 31%.  |
|
|
|
|
 Записан
Записан
|
Зачем откладывать на завтра то, что можно отложить на послезавтра?
|
|
|
|
